How Do You Think the Size of Atoms Will Change From Top to Bottom Within a Chemical Family?

7.three: Sizes of Atoms and Ions

1. Final updated

2. Save every bit PDF

Folio ID

21739

Learning Objectives

• To understand periodic trends in diminutive radii.
• To predict relative ionic sizes within an isoelectronic series.

Although some people autumn into the trap of visualizing atoms and ions as small, hard spheres like to miniature tabular array-lawn tennis balls or marbles, the quantum mechanical model tells us that their shapes and boundaries are much less definite than those images propose. Equally a result, atoms and ions cannot exist said to have exact sizes; however, some atoms are larger or smaller than others, and this influences their chemistry. In this section, we talk over how atomic and ion "sizes" are divers and obtained.

Atomic Radii

Recollect that the probability of finding an electron in the various available orbitals falls off slowly equally the distance from the nucleus increases. This indicate is illustrated in Figure \(\PageIndex{1}\) which shows a plot of total electron density for all occupied orbitals for iii noble gases as a part of their distance from the nucleus. Electron density diminishes gradually with increasing distance, which makes it impossible to draw a sharp line marking the purlieus of an atom.

Figure \(\PageIndex{1}\): Plots of Radial Probability as a Role of Altitude from the Nucleus for He, Ne, and Ar. In He, the 1s electrons have a maximum radial probability at ≈30 pm from the nucleus. In Ne, the anesouthward electrons have a maximum at ≈8 pm, and the twos and 2p electrons combine to course some other maximum at ≈35 pm (the north = ii shell). In Ar, the anesouth electrons have a maximum at ≈2 pm, the 2southward and iip electrons combine to form a maximum at ≈18 pm, and the iiidue south and 3p electrons combine to form a maximum at ≈70 pm.

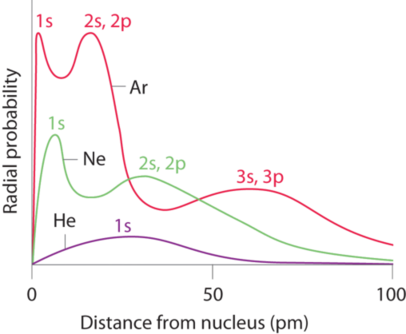
Effigy \(\PageIndex{i}\) too shows that there are distinct peaks in the total electron density at item distances and that these peaks occur at dissimilar distances from the nucleus for each chemical element. Each peak in a given plot corresponds to the electron density in a given principal shell. Because helium has only one filled trounce (n = i), it shows only a unmarried peak. In contrast, neon, with filled northward = one and 2 principal shells, has two peaks. Argon, with filled n = 1, two, and 3 chief shells, has three peaks. The peak for the filled n = 1 shell occurs at successively shorter distances for neon (Z = x) and argon (Z = 18) because, with a greater number of protons, their nuclei are more positively charged than that of helium. Because the 1southward ² shell is closest to the nucleus, its electrons are very poorly shielded by electrons in filled shells with larger values of n. Consequently, the two electrons in the northward = 1 shell experience nearly the full nuclear charge, resulting in a stiff electrostatic interaction between the electrons and the nucleus. The free energy of the n = ane shell too decreases tremendously (the filled 1southward orbital becomes more stable) equally the nuclear charge increases. For similar reasons, the filled north = 2 crush in argon is located closer to the nucleus and has a lower free energy than the n = two shell in neon.

Figure \(\PageIndex{1}\) illustrates the difficulty of measuring the dimensions of an individual atom. Because distances between the nuclei in pairs of covalently bonded atoms tin can be measured quite precisely, even so, chemists use these distances equally a basis for describing the approximate sizes of atoms. For instance, the internuclear distance in the diatomic Cl₂ molecule is known to be 198 pm. We assign half of this distance to each chlorine cantlet, giving chlorine a covalent diminutive radius (\(r_{cov}\)), which is half the distance between the nuclei of 2 like atoms joined by a covalent bond in the aforementioned molecule, of 99 pm or 0.99 Å (Figure \(\PageIndex{2a}\)). Atomic radii are often measured in angstroms (Å), a non-SI unit: ane Å = one × 10⁻¹⁰ g = 100 pm.

Figure \(\PageIndex{2}\): Definitions of the Atomic Radius. (a) The covalent atomic radius, r _cov, is half the distance between the nuclei of 2 like atoms joined by a covalent bond in the same molecule, such as Cl_two. (b) The metallic atomic radius, r _met, is one-half the distance between the nuclei of two adjacent atoms in a pure solid metal, such as aluminum. (c) The van der Waals atomic radius, r _vdW, is half the distance between the nuclei of two like atoms, such as argon, that are closely packed just non bonded. (d) This is a delineation of covalent versus van der Waals radii of chlorine. The covalent radius of Cl₂ is half the distance between the ii chlorine atoms in a single molecule of Cl_ii. The van der Waals radius is half the distance between chlorine nuclei in two unlike but touching Cl₂ molecules. Which do you think is larger? Why?

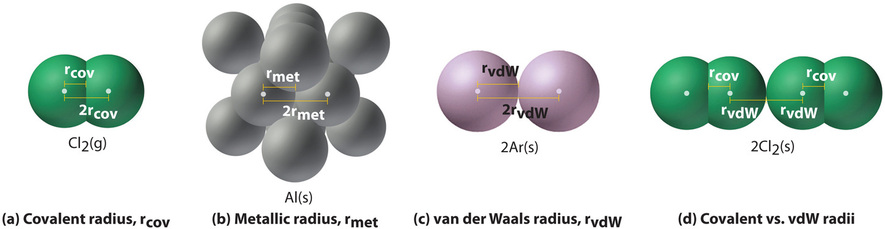
In a similar approach, we can employ the lengths of carbon–carbon single bonds in organic compounds, which are remarkably uniform at 154 pm, to assign a value of 77 pm as the covalent atomic radius for carbon. If these values practice indeed reverberate the actual sizes of the atoms, then nosotros should be able to predict the lengths of covalent bonds formed between different elements by adding them. For example, we would predict a carbon–chlorine altitude of 77 pm + 99 pm = 176 pm for a C–Cl bond, which is very close to the average value observed in many organochlorine compounds. A similar approach for measuring the size of ions is discussed later in this section.

Covalent atomic radii can be determined for most of the nonmetals, but how do chemists obtain atomic radii for elements that do not course covalent bonds? For these elements, a variety of other methods have been adult. With a metal, for example, the metallic atomic radius (\(r_{met}\)) is divers as half the altitude between the nuclei of two adjacent metal atoms in the solid (Figure \(\PageIndex{2b}\)). For elements such as the noble gases, most of which grade no stable compounds, we can utilize what is chosen the van der Waals atomic radius (\(r_{vdW}\)), which is half the internuclear distance between two nonbonded atoms in the solid (Effigy \(\PageIndex{2c}\)). This is somewhat hard for helium which does non form a solid at whatever temperature. An atom such as chlorine has both a covalent radius (the distance betwixt the two atoms in a \(\ce{Cl2}\) molecule) and a van der Waals radius (the distance between two Cl atoms in different molecules in, for example, \(\ce{Cl2(s)}\) at low temperatures). These radii are more often than not not the aforementioned (Figure \(\PageIndex{2nd}\)).

Periodic Trends in Atomic Radii

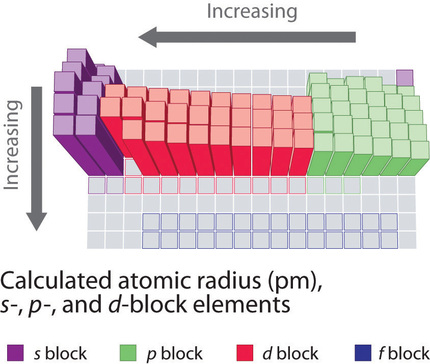
Because it is incommunicable to mensurate the sizes of both metal and nonmetallic elements using any 1 method, chemists have developed a self-consistent way of calculating atomic radii using the quantum mechanical functions. Although the radii values obtained by such calculations are not identical to any of the experimentally measured sets of values, they practice provide a way to compare the intrinsic sizes of all the elements and clearly evidence that atomic size varies in a periodic fashion (Effigy \(\PageIndex{3}\)).

Effigy \(\PageIndex{3}\): A Plot of Periodic Variation of Atomic Radius with Atomic Number for the First Six Rows of the Periodic Tabular array

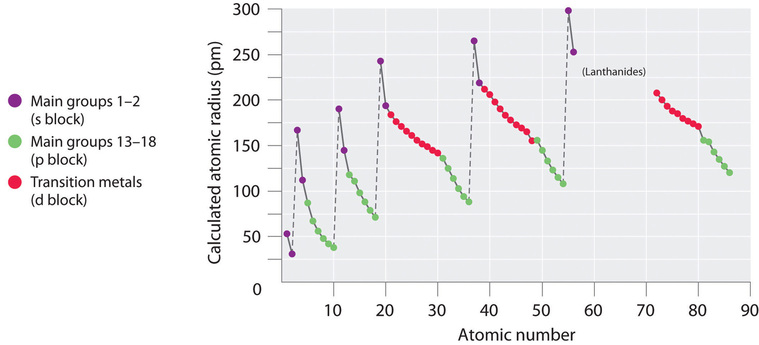
In the periodic tabular array, atomic radii decrease from left to right across a row and increase from top to bottom downwardly a column. Because of these ii trends, the largest atoms are found in the lower left corner of the periodic tabular array, and the smallest are plant in the upper right corner (Figure \(\PageIndex{4}\)).

Figure \(\PageIndex{4}\) Calculated Atomic Radii (in Picometers) of the s-, p-, and d-Cake Elements. The sizes of the circles illustrate the relative sizes of the atoms. The calculated values are based on quantum mechanical wave functions. Source: http://www.webelements.com. Web Elements is an excellent online source for looking up atomic properties.

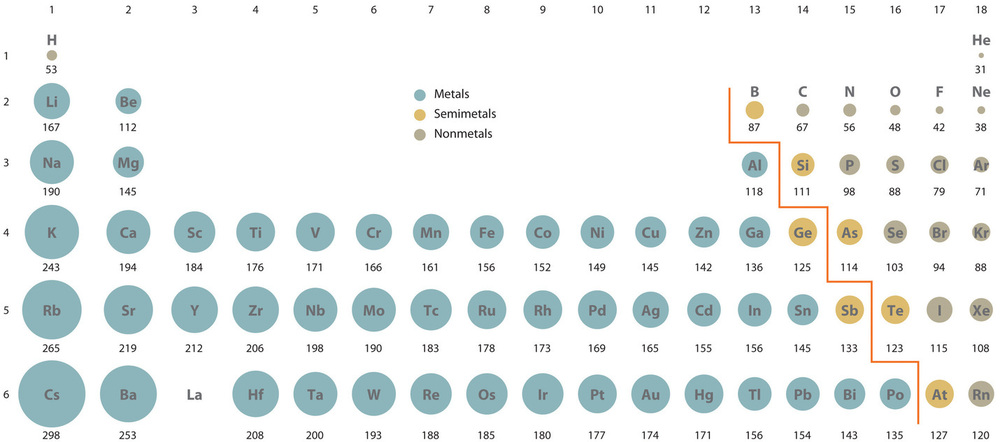
Trends in diminutive size result from differences in the constructive nuclear charges (\(Z_{eff}\)) experienced by electrons in the outermost orbitals of the elements. For all elements except H, the effective nuclear accuse is ever less than the actual nuclear charge because of shielding effects. The greater the effective nuclear charge, the more strongly the outermost electrons are attracted to the nucleus and the smaller the atomic radius.

Atomic radii decrease from left to right beyond a row and increment from top to lesser down a cavalcade.

The atoms in the 2nd row of the periodic table (Li through Ne) illustrate the result of electron shielding. All have a filled 1s ² inner shell, only as we go from left to right across the row, the nuclear charge increases from +3 to +ten. Although electrons are existence added to the 2s and 2p orbitals, electrons in the aforementioned principal shell are not very effective at shielding one another from the nuclear charge. Thus the unmarried 2southward electron in lithium experiences an effective nuclear accuse of approximately +1 considering the electrons in the filled 1s ² shell finer neutralize two of the three positive charges in the nucleus. (More than detailed calculations give a value of Z _eff = +ane.26 for Li.) In contrast, the two 2s electrons in beryllium practice not shield each other very well, although the filled 1s ⁱⁱ shell finer neutralizes ii of the 4 positive charges in the nucleus. This means that the effective nuclear accuse experienced by the 2s electrons in glucinium is betwixt +1 and +2 (the calculated value is +i.66). Consequently, beryllium is significantly smaller than lithium. Similarly, as we proceed across the row, the increasing nuclear charge is not effectively neutralized by the electrons being added to the 2due south and twop orbitals. The result is a steady increment in the effective nuclear accuse and a steady decrease in atomic size (Figure \(\PageIndex{5}\)).

Figure \(\PageIndex{5}\): The Atomic Radius of the Elements. The diminutive radius of the elements increases as we become from right to left across a period and equally we go down the periods in a grouping.

The increment in diminutive size going down a column is also due to electron shielding, merely the situation is more complex because the principal quantum number n is non constant. Equally we saw in Affiliate 2, the size of the orbitals increases as n increases, provided the nuclear accuse remains the same. In group 1, for instance, the size of the atoms increases substantially going down the cavalcade. It may at beginning seem reasonable to aspect this upshot to the successive add-on of electrons to ns orbitals with increasing values of n. Still, it is of import to retrieve that the radius of an orbital depends dramatically on the nuclear accuse. Every bit we go downwardly the cavalcade of the group 1 elements, the master quantum number n increases from 2 to vi, but the nuclear charge increases from +3 to +55!

As a upshot the radii of the lower electron orbitals in Cesium are much smaller than those in lithium and the electrons in those orbitals experience a much larger forcefulness of attraction to the nucleus. That strength depends on the constructive nuclear charge experienced by the the inner electrons. If the outermost electrons in cesium experienced the total nuclear charge of +55, a cesium cantlet would exist very small indeed. In fact, the effective nuclear charge felt by the outermost electrons in cesium is much less than expected (6 rather than 55). This ways that cesium, with a vis ^one valence electron configuration, is much larger than lithium, with a 2s ¹ valence electron configuration. The effective nuclear charge changes relatively niggling for electrons in the outermost, or valence shell, from lithium to cesium because electrons in filled inner shells are highly constructive at shielding electrons in outer shells from the nuclear charge. Even though cesium has a nuclear charge of +55, it has 54 electrons in its filled ones ²iis ⁱⁱ2p ^viiiis ²3p ^{half dozen}4due south ⁱⁱ3d ¹⁰4p ⁶vs ²fourd ¹⁰5p ⁶ shells, abbreviated equally [Xe]5south ²4d ¹⁰fivep ⁶, which effectively neutralize well-nigh of the 55 positive charges in the nucleus. The aforementioned dynamic is responsible for the steady increase in size observed every bit we go down the other columns of the periodic table. Irregularities tin can usually exist explained by variations in effective nuclear charge.

Not all Electrons shield every bit

Electrons in the same main shell are not very constructive at shielding 1 some other from the nuclear accuse, whereas electrons in filled inner shells are highly effective at shielding electrons in outer shells from the nuclear charge.

Example \(\PageIndex{1}\)

On the basis of their positions in the periodic table, adjust these elements in social club of increasing atomic radius: aluminum, carbon, and silicon.

Given: three elements

Asked for: adapt in order of increasing atomic radius

Strategy:

1. Identify the location of the elements in the periodic table. Determine the relative sizes of elements located in the same column from their principal breakthrough number n. Then make up one's mind the lodge of elements in the same row from their effective nuclear charges. If the elements are not in the same cavalcade or row, use pairwise comparisons.
2. Listing the elements in order of increasing diminutive radius.

Solution:

A These elements are not all in the same column or row, so nosotros must use pairwise comparisons. Carbon and silicon are both in grouping fourteen with carbon lying higher up, and so carbon is smaller than silicon (C < Si). Aluminum and silicon are both in the third row with aluminum lying to the left, then silicon is smaller than aluminum (Si < Al) because its effective nuclear accuse is greater.

B Combining the two inequalities gives the overall order: C < Si < Al.

Exercise \(\PageIndex{i}\)

On the basis of their positions in the periodic table, suit these elements in gild of increasing size: oxygen, phosphorus, potassium, and sulfur.

Reply

O < S < P < G

Atomic Radius: https://youtu.be/ZYKB8SNrGVY

Ionic Radii and Isoelectronic Serial

An ion is formed when either one or more electrons are removed from a neutral atom to form a positive ion (cation) or when additional electrons attach themselves to neutral atoms to class a negative i (anion). The designations cation or anion come up from the early experiments with electricity which found that positively charged particles were attracted to the negative pole of a bombardment, the cathode, while negatively charged ones were attracted to the positive pole, the anode.

Figure \(\PageIndex{half-dozen}\): Definition of Ionic Radius. (a) The internuclear distance is apportioned between adjacent cations (positively charged ions) and anions (negatively charged ions) in the ionic structure, as shown hither for Na⁺ and Cl⁻ in sodium chloride. (b) This delineation of electron density contours for a single aeroplane of atoms in the NaCl structure shows how the lines connect points of equal electron density. Note the relative sizes of the electron density contour lines around Cl⁻ and Na⁺.

Ionic compounds consist of regular repeating arrays of alternating positively charged cations and negatively charges anions. Although it is not possible to measure out an ionic radius directly for the same reason it is not possible to direct measure an atom's radius, it is possible to mensurate the altitude between the nuclei of a cation and an adjacent anion in an ionic chemical compound to determine the ionic radius (the radius of a cation or anion) of one or both. As illustrated in Effigy \(\PageIndex{6}\), the internuclear altitude corresponds to the sum of the radii of the cation and anion. A variety of methods have been developed to divide the experimentally measured distance proportionally between the smaller cation and larger anion. These methods produce sets of ionic radii that are internally consistent from 1 ionic compound to some other, although each method gives slightly different values. For example, the radius of the Na⁺ ion is essentially the aforementioned in NaCl and Na₂S, as long as the same method is used to measure it. Thus despite minor differences due to methodology, sure trends can exist observed.

A comparison of ionic radii with atomic radii (Figure \(\PageIndex{7}\)) shows that a cation, having lost an electron, is e'er smaller than its parent neutral atom, and an anion, having gained an electron, is e'er larger than the parent neutral atom. When 1 or more electrons is removed from a neutral atom, two things happen: (1) repulsions between electrons in the same principal shell decrease because fewer electrons are present, and (2) the effective nuclear accuse felt by the remaining electrons increases considering there are fewer electrons to shield one some other from the nucleus. Consequently, the size of the region of space occupied by electrons decreases and the ion shrinks (compare Li at 167 pm with Li⁺ at 76 pm). If different numbers of electrons can be removed to produce ions with different charges, the ion with the greatest positive charge is the smallest (compare Atomic number 26^{2 +} at 78 pm with Iron^{3 +} at 64.5 pm). Conversely, calculation one or more electrons to a neutral atom causes electron–electron repulsions to increase and the constructive nuclear accuse to subtract, so the size of the probability region increases and the ion expands (compare F at 42 pm with F⁻ at 133 pm).

Figure \(\PageIndex{7}\): Ionic Radii (in Picometers) of the Virtually Common Ionic States of the s-, p-, and d-Cake Elements.Gray circles betoken the sizes of the ions shown; colored circles indicate the sizes of the neutral atoms. Source: Ionic radius information from R. D. Shannon, "Revised constructive ionic radii and systematic studies of interatomic distances in halides and chalcogenides," Acta Crystallographica 32, no. 5 (1976): 751–767.

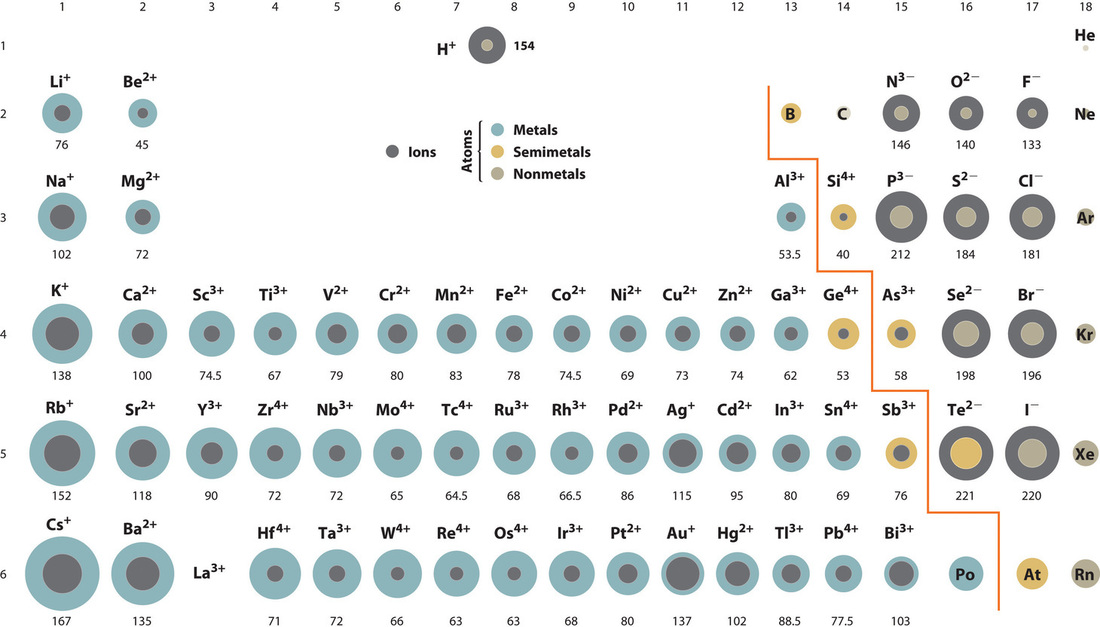
Cations are e'er smaller than the neutral cantlet and anions are e'er larger.

Because most elements grade either a cation or an anion simply not both, there are few opportunities to compare the sizes of a cation and an anion derived from the same neutral cantlet. A few compounds of sodium, however, contain the Na⁻ ion, allowing comparing of its size with that of the far more than familiar Na⁺ ion, which is institute in many compounds. The radius of sodium in each of its 3 known oxidation states is given in Tabular array \(\PageIndex{1}\). All three species have a nuclear charge of +11, just they contain 10 (Na⁺), 11 (Na⁰), and 12 (Na⁻) electrons. The Na⁺ ion is significantly smaller than the neutral Na atom because the 3s ^ane electron has been removed to requite a closed shell with n = 2. The Na⁻ ion is larger than the parent Na atom because the additional electron produces a iiis ² valence electron configuration, while the nuclear charge remains the same.

Table \(\PageIndex{one}\): Experimentally Measured Values for the Radius of Sodium in Its 3 Known Oxidation States

	Na+	Na0	Na−
Electron Configuration	1south 22due south 2twop 6	1s two2s 22p 63s one	anes 2twosouthward 22p 63s ii
Radius (pm)	102	154*	202†
*The metallic radius measured for Na(s). †Source: Yard. J. Wagner and J. L. Dye, "Alkalides, Electrides, and Expanded Metals," Annual Review of Materials Science 23 (1993): 225–253.

Ionic radii follow the aforementioned vertical tendency as diminutive radii; that is, for ions with the same charge, the ionic radius increases going down a column. The reason is the aforementioned as for atomic radii: shielding by filled inner shells produces little change in the constructive nuclear charge felt by the outermost electrons. Again, principal shells with larger values of n lie at successively greater distances from the nucleus.

Because elements in different columns tend to form ions with unlike charges, it is not possible to compare ions of the same charge beyond a row of the periodic table. Instead, elements that are side by side to each other tend to grade ions with the aforementioned number of electrons merely with different overall charges because of their different diminutive numbers. Such a set of species is known as an isoelectronic series. For example, the isoelectronic series of species with the neon airtight-shell configuration (1s ²twos ²2p ⁶) is shown in Table \(\PageIndex{3}\).

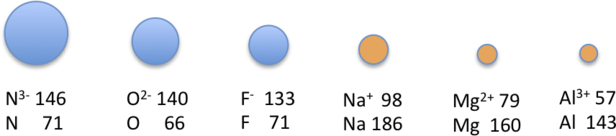
The sizes of the ions in this series decrease smoothly from Nⁱⁱⁱ⁻ to Al^{3 +}. All vi of the ions contain 10 electrons in the onedue south, twosouth, and iip orbitals, only the nuclear accuse varies from +vii (N) to +thirteen (Al). Every bit the positive accuse of the nucleus increases while the number of electrons remains the same, there is a greater electrostatic attraction between the electrons and the nucleus, which causes a decrease in radius. Consequently, the ion with the greatest nuclear charge (Al^{3 +}) is the smallest, and the ion with the smallest nuclear charge (N³⁻) is the largest. The neon cantlet in this isoelectronic series is not listed in Table \(\PageIndex{iii}\), because neon forms no covalent or ionic compounds and hence its radius is difficult to measure.

Tabular array \(\PageIndex{3}\): Radius of Ions with the Neon Closed-Trounce Electron Configuration. Source: R. D. Shannon, "Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides," Acta Crystallographica 32, no. v (1976): 751–767.

Ion	Radius (pm)	Atomic Number
North3−	146	vii
Oii−	140	8
F−	133	9
Na+	98	xi
Mgii +	79	12
Al3 +	57	13

Example \(\PageIndex{2}\)

Based on their positions in the periodic tabular array, adjust these ions in social club of increasing radius: Cl⁻, Thousand⁺, S²⁻, and Se²⁻.

Given: four ions

Asked for: order past increasing radius

Strategy:

1. Determine which ions form an isoelectronic series. Of those ions, predict their relative sizes based on their nuclear charges. For ions that practise not form an isoelectronic series, locate their positions in the periodic table.
2. Make up one's mind the relative sizes of the ions based on their principal quantum numbers northward and their locations within a row.

Solution:

A Nosotros run across that Southward and Cl are at the right of the third row, while K and Se are at the far left and correct ends of the fourth row, respectively. G⁺, Cl⁻, and S²⁻ form an isoelectronic series with the [Ar] closed-vanquish electron configuration; that is, all three ions contain 18 electrons but have unlike nuclear charges. Because Thou⁺ has the greatest nuclear charge (Z = 19), its radius is smallest, and Due south²⁻ with Z = 16 has the largest radius. Because selenium is directly below sulfur, we expect the Seⁱⁱ⁻ ion to be fifty-fifty larger than Southward²⁻.

B The club must therefore be M⁺ < Cl⁻ < S²⁻ < Se²⁻.

Exercise \(\PageIndex{2}\)

Based on their positions in the periodic table, arrange these ions in guild of increasing size: Br⁻, Ca^{2 +}, Rb⁺, and Sr^{ii +}.

Answer

Ca^{2 +} < Sr^{2 +} < Rb⁺ < Br⁻

Summary

Ionic radii share the same vertical trend as atomic radii, but the horizontal trends differ due to differences in ionic charges. A variety of methods have been established to measure the size of a single atom or ion. The covalent atomic radius ( r _cov ) is half the internuclear distance in a molecule with ii identical atoms bonded to each other, whereas the metal atomic radius ( r _met ) is defined equally one-half the altitude between the nuclei of 2 adjacent atoms in a metallic chemical element. The van der Waals radius ( r _vdW ) of an element is half the internuclear distance between two nonbonded atoms in a solid. Atomic radii decrease from left to correct across a row because of the increase in effective nuclear accuse due to poor electron screening by other electrons in the same principal vanquish. Moreover, atomic radii increase from top to bottom down a cavalcade because the effective nuclear charge remains relatively constant as the master quantum number increases. The ionic radii of cations and anions are always smaller or larger, respectively, than the parent cantlet due to changes in electron–electron repulsions, and the trends in ionic radius parallel those in atomic size. A comparison of the dimensions of atoms or ions that take the aforementioned number of electrons but different nuclear charges, called an isoelectronic series, shows a clear correlation between increasing nuclear accuse and decreasing size.

tranmustoom00.blogspot.com

Source: https://chem.libretexts.org/Bookshelves/General_Chemistry/Map:_Chemistry_-_The_Central_Science_%28Brown_et_al.%29/07._Periodic_Properties_of_the_Elements/7.3:_Sizes_of_Atoms_and_Ions

Share this post